1014 字

5 分钟

阅读量 --

二维计算几何模板

2021-12-14

算法

计算几何

算法

前提条件#

1
#include <iostream>
2
#include <cmath>
3
#include <algorithm>
4
using namespace std;
5
typedef double temType; // 需要用到的类型

点（向量）#

已知#

$(x,y)$ ，点坐标或向量坐标

函数#

相加、相减、与常数相加、点乘、叉乘、旋转、标准化

向量旋转#

\begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x\cos\theta-y\sin\theta \\ x\sin\theta+y\cos\theta \end{bmatrix}

代码#

1
// 点或向量
2
struct point{
3
    temType x, y;
4
    point(): x(0), y(0){}
5
    point(temType _x, temType _y): x(_x), y(_y){}
6
    point(const point &t){x = t.x;y = t.y;};
7
    point operator-(const point& t) const{return {x-t.x, y-t.y};}   // 相减
8
    point operator+(const point& t) const{return {t.x+x, t.y+y};}   // 相加
9
    point operator*(temType t) const{return {x*t, y*t};}            // 与常数相乘
10
    temType cdot(const point& t) const{return t.x*x+t.y*y;}                // 点乘
11
    temType times(const point& t) const{return x*t.y-y*t.x;}               // 叉乘
12
    bool operator==(const point& t) const{return x==t.x && y==t.y;}
13
    bool operator!=(const point& t) const{return x!=t.x || y!=t.y;}
14
    temType length() const{return sqrt(x*x+y*y); }
15
    void normalize() {                                                  //标准化
16
        temType sqt = sqrt(x*x+y*y);
17
        x = x/sqt; y = y/sqt;
18
    }
19
    point rotation(temType t) const{                                    //向量旋转
20
        temType cost=cos(t), sint=sin(t);
21
        return {x*cost-y*sint, x*sint+y*cost};
22
    }
23
};
24
typedef struct point pit;
25
typedef struct point vtr;

极坐标点#

1
struct polar{
2
    temType p, e;
3
    polar(temType _p, temType _e): p(_p), e(_e){}
4
};
5
typedef struct polar plr;
6

7
polar toPolar(const pit& t){ return {sqrt(t.x*t.x+t.y*t.y),atan2(t.y,t.x)}; }
8
pit toRect(const plr& t){ return {t.p*cos(t.e), t.p*sin(t.e)}; }

线段#

已知#

已知线段两端端点 $A,B$

函数#

跨立实验，快速排斥实验

代码#

1
// 线段
2
struct segment{
3
    pit A, B;
4
    segment(const pit& _A, const pit& _B): A(_A), B(_B){}
5
    pit midpoint() const{return {(A.x+B.x)/2.0, (A.y,B.y)/2.0};} // 中点
6
    bool rapidRejectionExp(const segment& t) const { // 快速排斥实验 TODO 这里有一些错误
7
        pit minTmp(min(A.x, B.x), min(A.y, B.y));
8
        pit maxTmp(max(A.x, B.x), max(A.y, B.y));
9
        return  (t.A.x >= minTmp.x && t.A.x <= maxTmp.x) && (t.A.y >= minTmp.y && t.A.y <= maxTmp.y) ||
10
                (t.B.x >= minTmp.x && t.B.x <= maxTmp.x) && (t.B.y >= minTmp.y && t.B.y <= maxTmp.y);
11
    }
12
    bool straddleExp(const segment& t) const{ // 跨立实验
13
//        if(!rapidRejectionExp(t)) return false;
14
        vtr AB = B-A, tba = t.A-t.B;
15
        temType t1 = AB.times(t.A-A) * AB.times(t.B-A), t2 = tba.times(A-t.B)*tba.times(B-t.B);
16
        if(t1 < 0 && t2 < 0) return true;
17
        else return false;
18
    }
19
};
20
typedef struct segment seg;

直线与射线#

已知#

已知直线上一点和向量， $P,\vec{s}$

函数#

获得直线上的一点

求两直线交点#

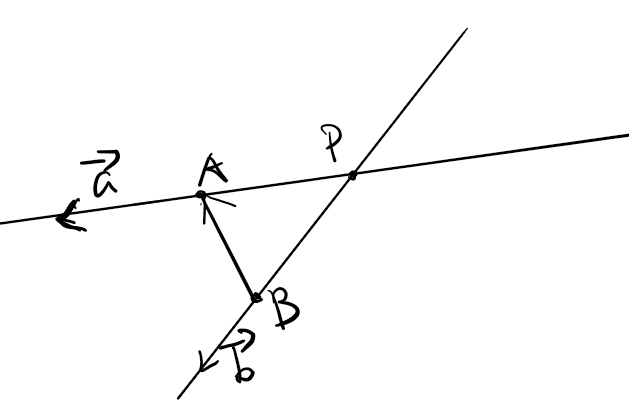
公式

P=A-\frac{\vec{b}\cdot\vec{BA}}{\vec{b}\cdot\vec{a}}\cdot\vec{a}

代码#

1
struct line{
2
    pit P;
3
    vtr s;
4
    line(const pit& _P, const vtr& _s): P(_P), s(_s) {s.normalize();}
5
    pit getPoint(temType t) const {return P + s*t;}
6
    bool ispParallel(const line& t) const{return s.times(t.s)==0;} // 平行
7
    bool isCoincide(const line& t) const{return s.times(t.s)==0 && ((s.times(P-t.P)==0));} // 重合
8
    pit intersection(const line& t) const{ return P - s * (t.s.times(P-t.P) / t.s.times(s)); }
9
};
10
typedef struct line line; // 直线
11
typedef struct line ray; // 射线

圆#

已知#

圆心 $O$ ，半径 $r$

代码#

1
struct circle{
2
    pit O;
3
    temType r;
4
    circle(const pit& _O, temType _r): O(_O), r(_r){}
5
};
6
typedef struct circle cle;

直线与圆#

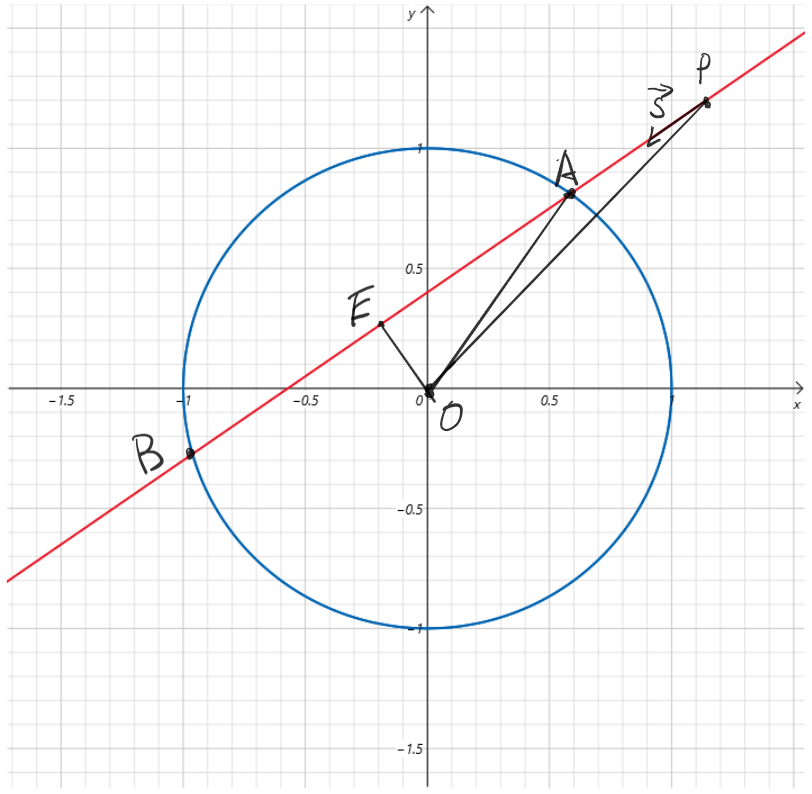
已知#

直线： $P$ 点坐标 $(P_x,P_y)$ ， $\vec{s}=(s_x,s_y)$

圆： $O$ 点坐标 $(O_x,O_y)$ ，圆的半径 $r$

推导#

|OE|= \frac{\vec{s} \times \vec{PO}}{|\vec{s}|} \\ |PE|= \frac{\vec{s} \cdot \vec{PO}}{|\vec{s}|}\\ |AE|=|BE|=\sqrt{r^2-|OE|^2}\\ |PA|=|PE|-|AE|\\ |PB|=|PE|+|BE|\\ A=P+\frac{|PA|}{|\vec{s}|}\cdot\vec{s}\\ B=P+\frac{|PB|}{|\vec{s}|}\cdot\vec{s}

代码#

1
seg intersectionOfLineAndCircle(const line& p, const cle& c){
2
    vtr PO = c.O - p.P;
3
    temType OE = p.s.times(PO), PE = p.s.times(PO);
4
    temType tmp = sqrt(c.r*c.r-OE*OE);
5
    return {p.getPoint(PE-tmp), p.getPoint(PE+tmp)};
6
}

凸包#

已知#

已知一个二维坐标图中每个顶点，求最小周长能够包含所有所有顶点的凸包

思路#

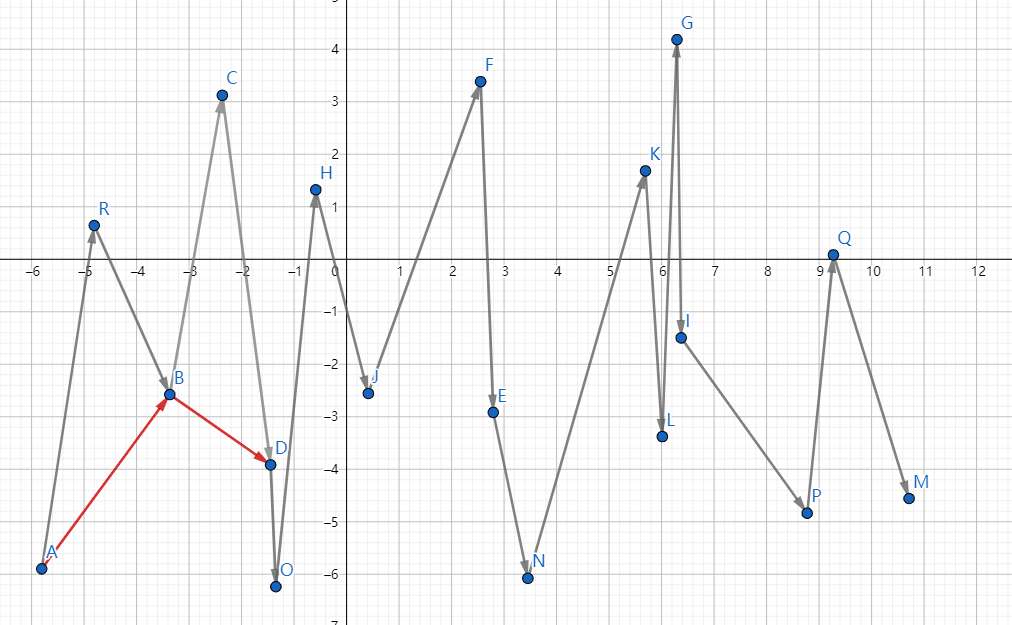
先将点双关键字排序，横坐标为第一关键字，纵坐标为第二关键字

排序之后

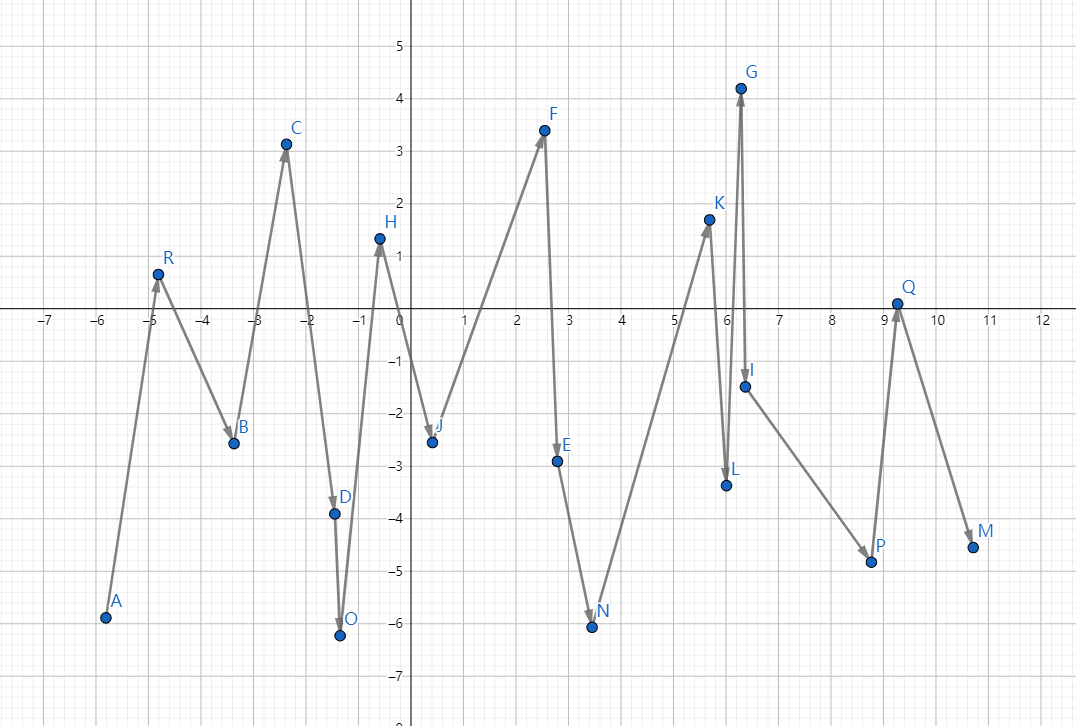
图片向量方向迭代方向

之后维护单调单调栈，其中栈顶为 $S_1$ ，栈顶第二元素为 $S_2$ ，当前检查的点为 $P$ ，由于凸包是不会出现右转的，所以当出现 $\vec{S_2S_1}\times\vec{S_1P}<0$ 说明栈顶的元素不是最优凸包，弹出栈顶重复上一步。

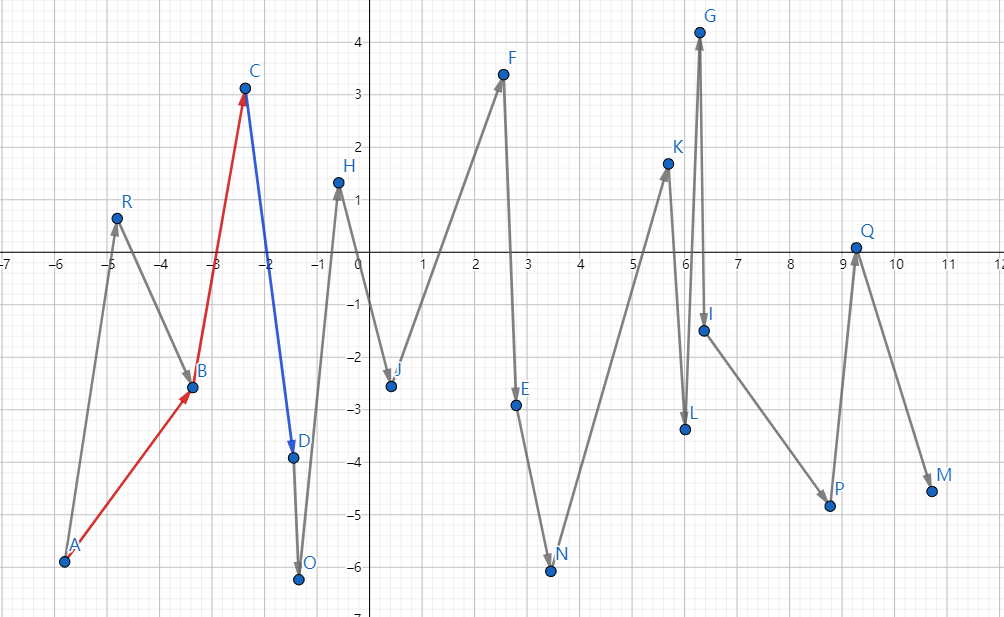
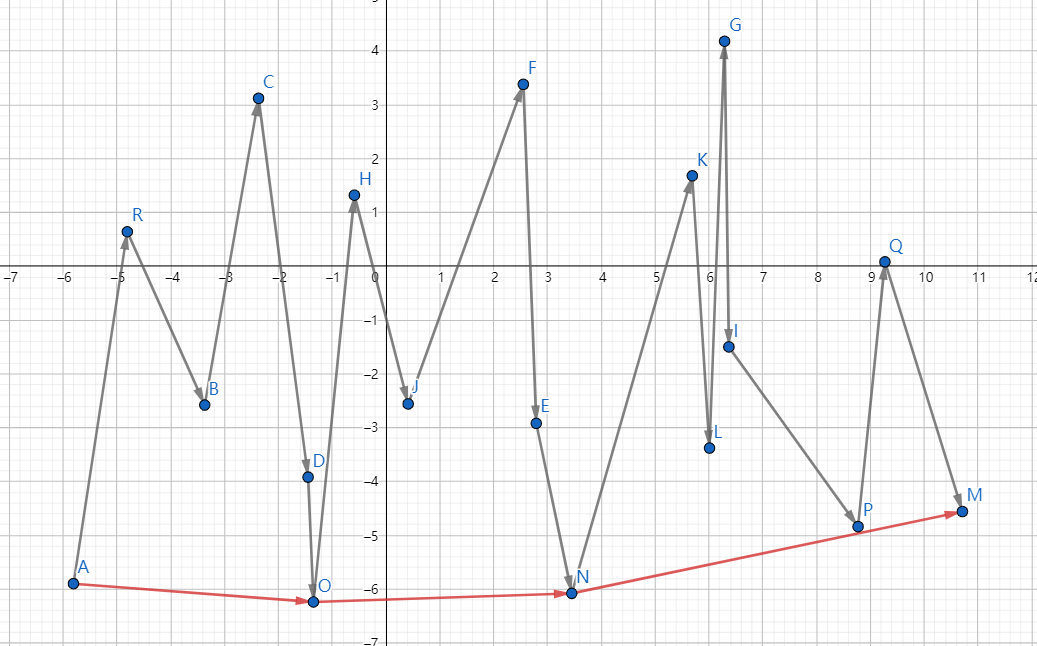
第一次循环迭代之后，会发现求完了下凸包先在需要倒转迭代方向，再次遍历

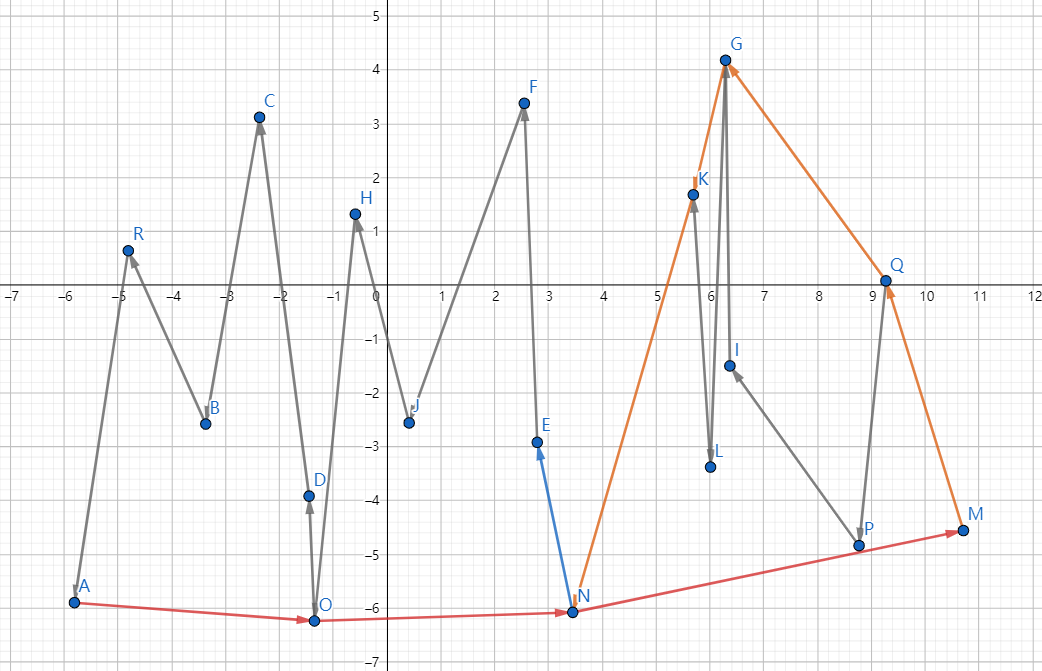
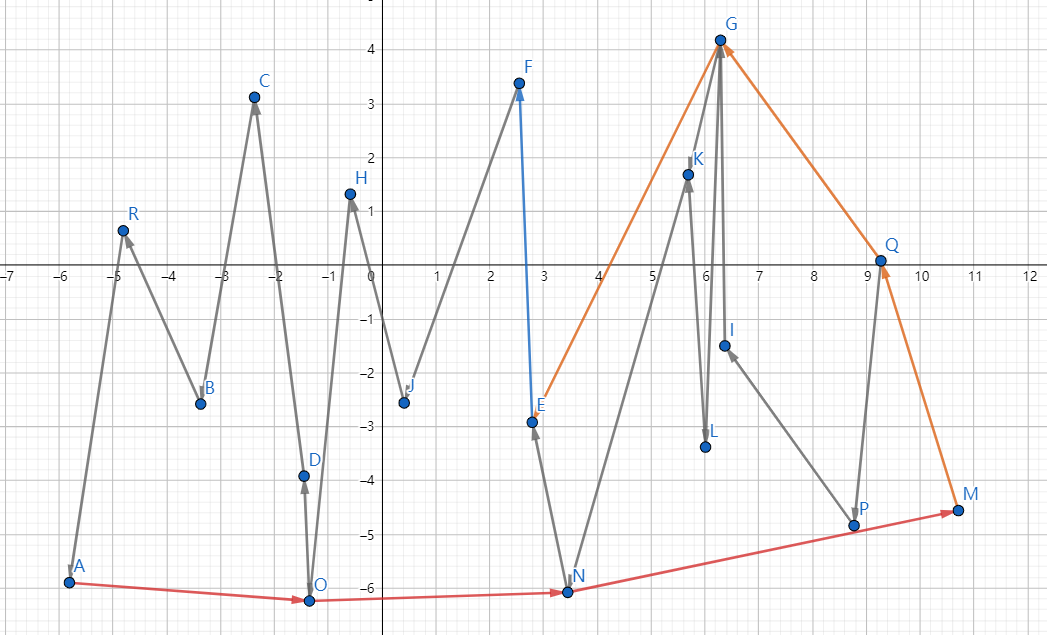
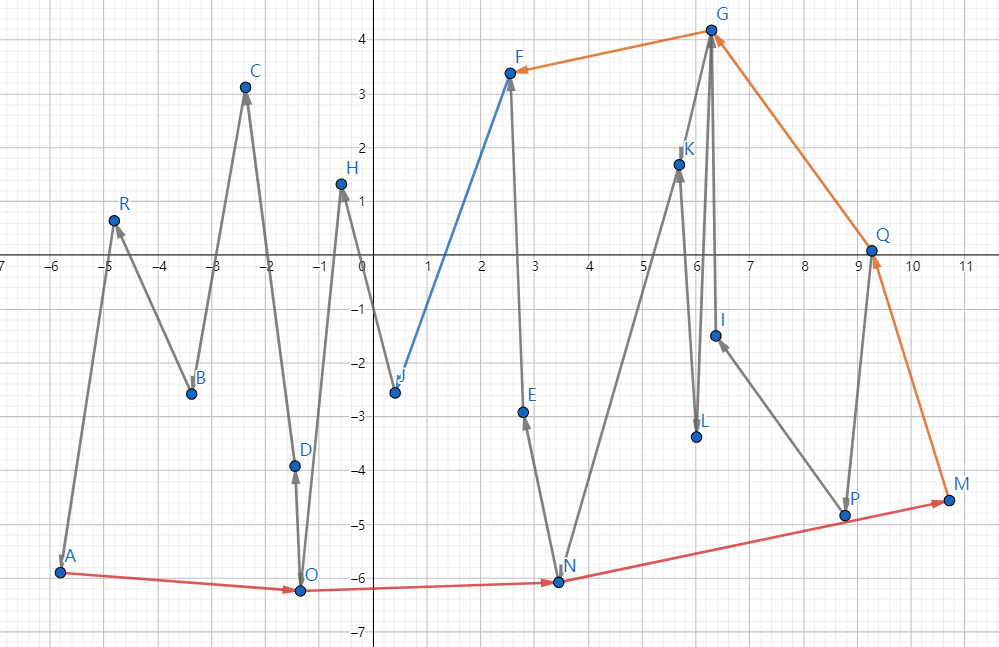
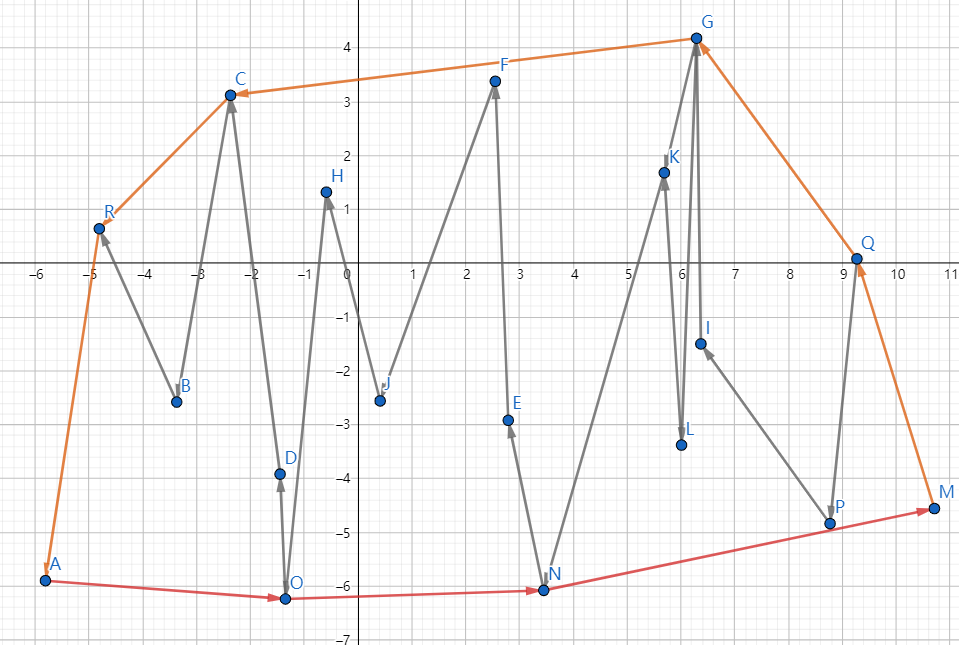
第二次迭代完善上凸包，最终会形成一个最短周长的能够包含所有顶点的凸包

注意：运行结果最后还会添加一次初始节点，那么周长就为 $\sum_{i=0}^{tp-1}|\vec{p_ip_{i+1}}|$

代码#

1
const int N = 1e5+10;
2
pit p[N];
3
int stk[N<<1];
4
int tp;
5

6
bool cmp(pit &a, pit &b){
7
    if(a.x == b.x) return a.y < b.y;
8
    return a.x < b.x;
9
}
10

11
int main() {
12
    debug;
13
    int n;
14
    temType xt, yt;
15
    cin >> n;
16
    for(int i = 0; i < n; ++i) {
17
        cin >> xt >> yt;
18
        p[i] = point(xt, yt);
19
    }
20
    sort(p, p+n, cmp);
21
    stk[++tp] = 0;
22
    for(int i = 1; i < n; ++i) {
23
        while (tp >= 2 && ((p[stk[tp]]-p[stk[tp-1]]).times(p[i]-p[stk[tp]]) < 0)) tp--;
24
        stk[++tp] = i;
25
    }
26
    int tmp = tp;
27
    for(int i = n-1; i >= 0; --i){
28
        while (tp > tmp && ((p[stk[tp]]-p[stk[tp-1]]).times(p[i]-p[stk[tp]]) < 0)) tp--;
29
        stk[++tp] = i;
30
    }
31
    temType ans = 0;
32
    for(int i = 1; i <= tp; ++i) {
33
        ans += (p[stk[i]] - p[stk[i-1]]).length();
34
    }
35
    printf("%.2f", ans);
36
}

Translate by Kimi-K3

Prerequisites#

1
#include <iostream>
2
#include <cmath>
3
#include <algorithm>
4
using namespace std;
5
typedef double temType; // the type we will use

Point (Vector)#

Given#

$(x,y)$ , the coordinates of a point or a vector

Operations#

Addition, subtraction, addition with a constant, dot product, cross product, rotation, normalization

Vector Rotation#

\begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x\cos\theta-y\sin\theta \\ x\sin\theta+y\cos\theta \end{bmatrix}

Code#

1
// point or vector
2
struct point{
3
    temType x, y;
4
    point(): x(0), y(0){}
5
    point(temType _x, temType _y): x(_x), y(_y){}
6
    point(const point &t){x = t.x;y = t.y;};
7
    point operator-(const point& t) const{return {x-t.x, y-t.y};}   // subtraction
8
    point operator+(const point& t) const{return {t.x+x, t.y+y};}   // addition
9
    point operator*(temType t) const{return {x*t, y*t};}            // multiplication by a constant
10
    temType cdot(const point& t) const{return t.x*x+t.y*y;}                // dot product
11
    temType times(const point& t) const{return x*t.y-y*t.x;}               // cross product
12
    bool operator==(const point& t) const{return x==t.x && y==t.y;}
13
    bool operator!=(const point& t) const{return x!=t.x || y!=t.y;}
14
    temType length() const{return sqrt(x*x+y*y); }
15
    void normalize() {                                                  //normalization
16
        temType sqt = sqrt(x*x+y*y);
17
        x = x/sqt; y = y/sqt;
18
    }
19
    point rotation(temType t) const{                                    //vector rotation
20
        temType cost=cos(t), sint=sin(t);
21
        return {x*cost-y*sint, x*sint+y*cost};
22
    }
23
};
24
typedef struct point pit;
25
typedef struct point vtr;

Point in Polar Coordinates#

1
struct polar{
2
    temType p, e;
3
    polar(temType _p, temType _e): p(_p), e(_e){}
4
};
5
typedef struct polar plr;
6

7
polar toPolar(const pit& t){ return {sqrt(t.x*t.x+t.y*t.y),atan2(t.y,t.x)}; }
8
pit toRect(const plr& t){ return {t.p*cos(t.e), t.p*sin(t.e)}; }

Segment#

Given#

The two endpoints $A,B$ of the segment are known

Operations#

Straddle test, rapid rejection test

Code#

1
// segment
2
struct segment{
3
    pit A, B;
4
    segment(const pit& _A, const pit& _B): A(_A), B(_B){}
5
    pit midpoint() const{return {(A.x+B.x)/2.0, (A.y,B.y)/2.0};} // midpoint
6
    bool rapidRejectionExp(const segment& t) const { // rapid rejection test TODO there are some errors here
7
        pit minTmp(min(A.x, B.x), min(A.y, B.y));
8
        pit maxTmp(max(A.x, B.x), max(A.y, B.y));
9
        return  (t.A.x >= minTmp.x && t.A.x <= maxTmp.x) && (t.A.y >= minTmp.y && t.A.y <= maxTmp.y) ||
10
                (t.B.x >= minTmp.x && t.B.x <= maxTmp.x) && (t.B.y >= minTmp.y && t.B.y <= maxTmp.y);
11
    }
12
    bool straddleExp(const segment& t) const{ // straddle test
13
//        if(!rapidRejectionExp(t)) return false;
14
        vtr AB = B-A, tba = t.A-t.B;
15
        temType t1 = AB.times(t.A-A) * AB.times(t.B-A), t2 = tba.times(A-t.B)*tba.times(B-t.B);
16
        if(t1 < 0 && t2 < 0) return true;
17
        else return false;
18
    }
19
};
20
typedef struct segment seg;

Line and Ray#

Given#

A point on the line and a vector are known, $P,\vec{s}$

Operations#

Get a point on the line

Finding the Intersection of Two Lines#

Formula

P=A-\frac{\vec{b}\cdot\vec{BA}}{\vec{b}\cdot\vec{a}}\cdot\vec{a}

Code#

1
struct line{
2
    pit P;
3
    vtr s;
4
    line(const pit& _P, const vtr& _s): P(_P), s(_s) {s.normalize();}
5
    pit getPoint(temType t) const {return P + s*t;}
6
    bool ispParallel(const line& t) const{return s.times(t.s)==0;} // parallel
7
    bool isCoincide(const line& t) const{return s.times(t.s)==0 && ((s.times(P-t.P)==0));} // coincident
8
    pit intersection(const line& t) const{ return P - s * (t.s.times(P-t.P) / t.s.times(s)); }
9
};
10
typedef struct line line; // line
11
typedef struct line ray; // ray

Circle#

Given#

Center $O$ , radius $r$

Code#

1
struct circle{
2
    pit O;
3
    temType r;
4
    circle(const pit& _O, temType _r): O(_O), r(_r){}
5
};
6
typedef struct circle cle;

Line and Circle#

Given#

Line: coordinates of point $P$ $(P_x,P_y)$ , $\vec{s}=(s_x,s_y)$

Circle: coordinates of point $O$ $(O_x,O_y)$ , radius of the circle $r$

Derivation#

|OE|= \frac{\vec{s} \times \vec{PO}}{|\vec{s}|} \\ |PE|= \frac{\vec{s} \cdot \vec{PO}}{|\vec{s}|}\\ |AE|=|BE|=\sqrt{r^2-|OE|^2}\\ |PA|=|PE|-|AE|\\ |PB|=|PE|+|BE|\\ A=P+\frac{|PA|}{|\vec{s}|}\cdot\vec{s}\\ B=P+\frac{|PB|}{|\vec{s}|}\cdot\vec{s}

Code#

1
seg intersectionOfLineAndCircle(const line& p, const cle& c){
2
    vtr PO = c.O - p.P;
3
    temType OE = p.s.times(PO), PE = p.s.times(PO);
4
    temType tmp = sqrt(c.r*c.r-OE*OE);
5
    return {p.getPoint(PE-tmp), p.getPoint(PE+tmp)};
6
}

Convex Hull#

Given#

Given every vertex in a 2D coordinate plane, find the convex hull with the minimum perimeter that contains all the vertices

Approach#

First sort the points by two keys, with the x-coordinate as the primary key and the y-coordinate as the secondary key

After sorting

The vector direction in the picture is the iteration direction

Then maintain a monotonic stack, where the top of the stack is $S_1$ , the second element from the top is $S_2$ , and the point currently being checked is $P$ . Since a convex hull never makes a right turn, when $\vec{S_2S_1}\times\vec{S_1P}<0$ it means the element at the top of the stack is not part of the optimal convex hull, so pop the top and repeat the previous step.

After the first iteration, you will find that the lower hull has been computed; now you need to reverse the iteration direction and traverse again

The second iteration completes the upper hull, eventually forming a convex hull with the shortest perimeter that contains all vertices

Note: the result will add the initial node once more at the end, so the perimeter is $\sum_{i=0}^{tp-1}|\vec{p_ip_{i+1}}|$

Code#

1
const int N = 1e5+10;
2
pit p[N];
3
int stk[N<<1];
4
int tp;
5

6
bool cmp(pit &a, pit &b){
7
    if(a.x == b.x) return a.y < b.y;
8
    return a.x < b.x;
9
}
10

11
int main() {
12
    debug;
13
    int n;
14
    temType xt, yt;
15
    cin >> n;
16
    for(int i = 0; i < n; ++i) {
17
        cin >> xt >> yt;
18
        p[i] = point(xt, yt);
19
    }
20
    sort(p, p+n, cmp);
21
    stk[++tp] = 0;
22
    for(int i = 1; i < n; ++i) {
23
        while (tp >= 2 && ((p[stk[tp]]-p[stk[tp-1]]).times(p[i]-p[stk[tp]]) < 0)) tp--;
24
        stk[++tp] = i;
25
    }
26
    int tmp = tp;
27
    for(int i = n-1; i >= 0; --i){
28
        while (tp > tmp && ((p[stk[tp]]-p[stk[tp-1]]).times(p[i]-p[stk[tp]]) < 0)) tp--;
29
        stk[++tp] = i;
30
    }
31
    temType ans = 0;
32
    for(int i = 1; i <= tp; ++i) {
33
        ans += (p[stk[i]] - p[stk[i-1]]).length();
34
    }
35
    printf("%.2f", ans);
36
}

二维计算几何模板

https://blog.csome.cc/p/cg-template/

作者

Csome

发布于

2021-12-14

许可协议

CC BY-SA 3.0

[TQLCTF]Pwn Tunbelievable_write wp

微调Hexo主题Anatolo接入gitalk